先日統計検定1級を受験し、統計数理に合格しました。
統計検定は今年から問題傾向が応用寄りに若干変化した印象を受け、難しく感じました。
この記事では、統計検定公式HPの以下の数字から、統計数理、統計応用で合格率に差があるのかを、母比率の差の検定で確かめます。(結論:合格率に差がありました)
データ
以下の数字は、統計検定公式HPを参考にいたしました。
統計数理 23.0%(合格者202、受験者878)
統計応用 15.8%(合格者125、受験者793)
| 統計数理 | 統計応用 | |
| 受験者 | 878 | 793 |
| 合格者 | 202 | 125 |
| 合格率 | 0.230068 | 0.157629 |
検定
統計数理、統計応用で合格率に差があるのかについて、母比率の差の検定をします。
帰無仮説 \(H_0\):「統計数理、統計応用で合格率に差がある」
について、有意水準\(\alpha = 0.05 \)で棄却されるかどうかを確かめます。
統計量
理論的な部分は、25-7. 母比率の差の検定(https://bellcurve.jp/statistics/course/18227.html)
を参考にしてください。エクセルで実装すると、下のようになり、サンプル数が十分が大きいと統計量\( z \)は、標準正規分布\( N(0, 1) \)に従います。
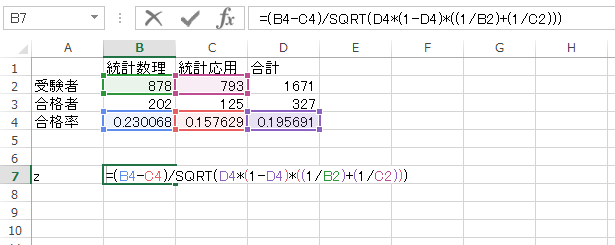
エクセルでこんな風に実装します。\( z \)の値は、3.727104と出ました。
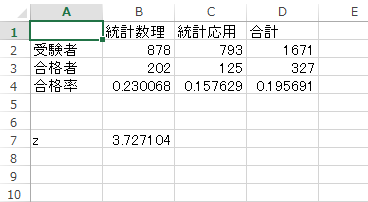
比率に差があるかなので、両側検定をします。
有意水準\(\alpha = 0.05 \)での棄却域は\( | Z | ≧ 1.96 \)より、帰無仮説は棄却されます。よって統計数理と統計応用の合格率に差があることになります。
有意水準は、0.01でも、0.005でも、0.001でも結論は同じ。 p値は約0.0002あたり。
参考:標準正規分布表(https://www.koka.ac.jp/morigiwa/sjs/standard_normal_distribution.htm)
そもそも母集団が同じ受験者混ざっているんだけどいいの?
受験者の大半は僕含めて統計数理と統計応用を同時に受けたりしたはず。
統計数理の合格率と統計応用の合格率には、おそらく正の相関があるのではないかと思いますが、公式サイトの情報からだとその正確な値は分かりません。
まあとりあえずわかる範囲での分析ってことで。

コメント