【改良版】パワポケの内部乱数観測器をPythonで実装してみた

パワポケシリーズは起動時間（時間：分：秒）をもとにした初期乱数シードから、古典的な線形合同で次の乱数を生成します。

そのため、起動時間とゲーム内の行動（というより乱数消費回数）が同じならば常に乱数消費によって起こるランダムイベントの内容を同一にすることが可能なため、いわゆる「乱数調整」「状況再現」をすることが可能となります。

それだけなら僕自身が1年前にすでにこちらの記事（パワポケシリーズ乱数とそのPythonでの実装による観測）で行っていますが、本記事ではプログラムの出力が効率的かつ見やすくなるように書き換えました。

なお、プログラム作成および記事執筆には、下の記事を参考にしました。

・パワポケ12　秘密結社編　乱数調整でMP装備が必ず作れるプログラム

・パワポケシリーズ乱数とそのPythonでの実装による観測

・パワポケ乱数値とオート命名の名前の関係

プログラム

言語はPythonです。コピペしてご自由にお使いください。

青色の解説部分は、適宜適切なパラメータに変えて実行してください。

# パワポケ乱数観測器

#1:ここで出力時の色を定義
class Color:
    RED = '\033[31m'
    YELLOW = '\033[33m'
    BLUE = '\033[34m'
    CYAN = '\033[36m'
    END = '\033[0m'

#2:オート命名とゲーム内部の乱数の関連付け
namelist = [
'佐藤','鈴木','高橋','田中','渡辺','伊藤','山本','中村','小林','加藤',
'松尾','菊地','野村','新井','渡部','佐野','杉本','大西','桜井','古川',
'吉田','山田','佐々木','斎藤','山口','松本','井上','木村','林','清水',
'山崎','池田','阿部','橋本','森','石川','中嶋','前田','小川','藤田',
'岡田','後藤','長谷川','石井','村上','近藤','坂本','遠藤','青木','藤井',
'西村','福田','三浦','藤原','岡本','松田','中川','中野','原田','小野',
'田村','竹内','金子','斎藤','和田','中山','石田','上田','森田','柴田',
'原','酒井','工藤','宮崎','横山','宮本','内田','高木','谷口','高田',
'丸山','今井','河野','小島','藤本','村田','武田','上野','杉山','増田',
'小山','大塚','平野','菅原','久保','千葉','松井','岩崎','木下','野口'
]

#3:DS初代かLiteでの起動時間。時間 h　分 m　秒 s
h = 0
m = 0
s = 10
#4:乱数生成回数、表示回数。
N = 500000
#5:線形合同法の実装
Y = 0    #6:←オート命名での重複判定に使う
X = h * (2 ** 16) + m * (2 ** 8) + s + 1
A = 0x5d588b656c078965
C = 0x0000000000269ec3
M = 2 ** 64
print(0, "番目 " ,0)
for i in range(0, N):
    Y = X
    X = (X * A + C) % M

    #7:乱数値で色分けして出力
    if 0 < X < 0.02 * M: #8:←裏サクセスの合成でMPができる場合の判定。11裏では0.005 * M、12裏では0.02 * M、それ以外は0でOK
        print(i+1, Color.RED + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
        print("MPだああああああああああああああああああああああああああああああああああああああああああああああああああああああああああああ")
    elif 0.02 * M < X < 0.2 * M: #9:←11裏では0.005 * M、12裏では0.02 * M、それ以外は0でOK
        print(i+1, Color.RED + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
    elif 0.2 * M < X < 0.4 * M:
        print(i+1, Color.YELLOW + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
    elif 0.8 * M < X < M:
        print(i+1, Color.BLUE + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
    elif 0.6 * M < X < 0.8 * M:
        print(i+1, Color.CYAN + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
    elif 0.4 * M < X < 0.6 * M:
        print(i+1, "★★ ",namelist[int(100*X/M)] , X/M)

    #10:オート命名が連続して同じになる場合はスキップ
    if (100 * Y / M) // 1 == (100* X / M) // 1:
        print("●スキップ●")

出力結果、プログラムの解説や実際のゲームの実行結果

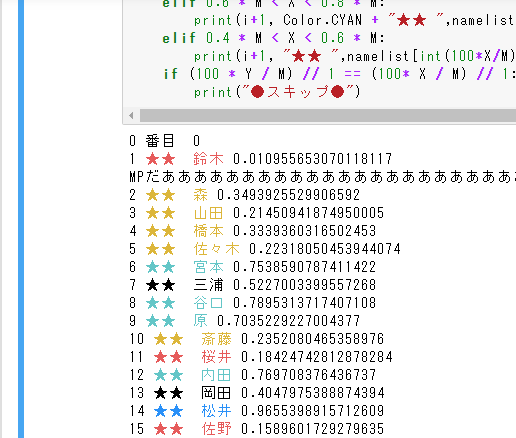
上のプログラムを実行した出力結果です。#1, #7で出力結果に色がついて見やすいようにしています。

一番左の数字が、乱数消費回数。

その右の名前は、オート命名をした時に対応するものです。小数第1, 2位の値と対応して決まります。例えば、0.00なら佐藤、0.01なら鈴木、・・・0.99なら野口と出ます。

（名前と数値の対応については、#2に実装しています。詳しくはこちら：パワポケ乱数値とオート命名の名前の関係）

名前の右は、乱数値。下の「#5：線形合同法の実装」の部分で生成されます。

パワポケの乱数生成の礎となるコア部分です。

#5:線形合同法の実装
Y = 0    #6:←オート命名での重複判定に使う
X = h * (2 ** 16) + m * (2 ** 8) + s + 1　#初期乱数シード
A = 0x5d588b656c078965　#線形合同法による次の乱数生成のためのパラメータ
C = 0x0000000000269ec3　#線形合同法による次の乱数生成のためのパラメータ
M = 2 ** 64　#線形合同法による次の乱数生成のためのパラメータ
print(0, "番目 " ,0)
for i in range(0, N):
    Y = X　#6:オート命名での重複判定に使う
    X = (X * A + C) % M　#線形合同法による次の乱数生成の式

Xの部分は、#3の起動時間で定めた値に従って生成される初期乱数シード（図で0番目にあたるもの。ほぼ0。具体的には0.0000000000001くらい）。

パワポケの乱数生成やそのパラメータについては、σ軸さんの【パワポケ９ TAS】乱数解析を駆使してブギウギ商店街で暴れまわる #1を参考にいたしました。

実機では、パワポケ10か11を00:00:10（#3のとおり）に起動してサクセス開始時の名前を決めるところでオート命名をすると、図のようになります。ぜひ試してみてください。（パワポケ12は途中のムービーで乱数が消費されるので別）

また、表示される乱数の個数は#4に書いた値のとおりになります。数が大きすぎると時間が少しかかるので注意。

オート命名では直前と同じ名前は出ない仕様なので、その場合は#6, #10で判定し、●スキップ●と出力します。

実際のゲームでも下の図の通り85番目から村田、高田の次は藤原となりますが、2回目の藤原はスキップ、代わりに小山が出ます。

85 村田→86 高田→87 藤原→88 藤原→89 小山と、88番目はスキップして89番目へ。（一回入力をやめてメニューに戻れば88番目もできます）

上の図のように、出力を乱数値が0-0.2, 0.2-0.4, 0.4-0.6, 0.6-0.8, 0.8-1で分けている（寒色ほど値が高い）のは、11裏や12裏の合成システムで使うとともに、値の高いものが欲しかったり、分かりやすくするためです。

また、#8, #9では11裏、12裏の合成システムで通常よりも強い装備であるMPを粘りたいときに使います。MPを生成する乱数のとき（11裏：0.5%、12裏：2%）は、「MPだあああ」と横に広く出力します。この部分は11裏、12裏用に使うか、それ以外の用途で使うかどうかで書き換えてください。

    #7:乱数値で色分けして出力
    if 0 < X < 0.02 * M: #8:←裏サクセスの合成でMPができる場合の判定。11裏では0.005 * M、12裏では0.02 * M、それ以外は0でOK
        print(i+1, Color.RED + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
        print("MPだああああああああああああああああああああああああああああああああああああああああああああああああああああああああああああ")
    elif 0.02 * M < X < 0.2 * M: #9:←11裏では0.005 * M、12裏では0.02 * M、それ以外は0でOK
        print(i+1, Color.RED + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
    elif 0.2 * M < X < 0.4 * M:
        print(i+1, Color.YELLOW + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
    elif 0.8 * M < X < M:
        print(i+1, Color.BLUE + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
    elif 0.6 * M < X < 0.8 * M:
        print(i+1, Color.CYAN + "★★ ",namelist[int(100*X/M)] + Color.END, X/M)
    elif 0.4 * M < X < 0.6 * M:
        print(i+1, "★★ ",namelist[int(100*X/M)] , X/M)

    #10:オート命名が連続して同じになる場合はスキップ
    if (100 * Y / M) // 1 == (100* X / M) // 1:
        print("●スキップ●")

#10

の部分で、オート命名の重複判定を行います。上の図であったとおり、連続する乱数（Y, X）の小数第1位と小数第2位がともに同じ場合はオート命名で違う名前になるまでスキップされます。

まとめ

・パワポケ乱数観測機を、乱数値やMP判定、スキップ判定ができる旧バージョンに対して、オート命名で出力される名前を新たに追加して分かりやすく、使いやすくしました

・実際のコードを示し、部分ごとの処理や役割、メカニズムを解説しました

ありがとうございました。