英検1級で一番難しいといわれているのが、語彙問題。
この語彙問題の選択肢に出てくる単語はかなり難解で、英検1級に1発で合格した僕でも半分近くの単語を知りませんでしたが、それでも合格だけならなんとかなる(なんとかした)という経験をもとに、お伝えします。
前提
英検1級の語彙問題は25問あり、すべて空所補充型の4択式問題で正解は必ず4つのうち1つです。25問のうち21問が単語問題、4問が熟語(単語+前置詞の形が多い)となります。
ここで重要なのが、4つの選択肢はすべて違う意味の単語、熟語であることが多いです。(意味が似ていて、用法や場面ごとの使い分けを問う問題もたまにあります)
認識できる選択肢の数と正解率の関係
前提として、ここでいう「認識できる」とは、その選択肢が問題の答えになるかどうかを確実に判断できる、というものだとします。
まず4択問題で認識できる選択肢の数と、その時の正解率は以下の通りです。
4択問題で、選択肢の単語が\(n\)個\((n=0,1,2,3,4)\)分かるときの正解率
長いので結論だけ見るのでもよいです。
(0)選択肢の単語が1個も認識できない場合
この場合は、ランダムに選ぶしかないので、正解率25%です。
(意味が分からないなりに単語の成り立ちを分析して雰囲気で選んだり、熟語なら前置詞から類推して選ぶなんてこともできたりしますが、ここでは考えないことにします)
(1)選択肢の単語が1個だけ認識できる場合
分かる選択肢1個が運よく正解のものなら正解率100%、分からない選択肢3個のどれかが正解なら正解率1/3です。
その単語が、意味が分かり正誤判定できる選択肢であることと、問題の正解となる選択肢であることが互いに独立である([A])と仮定すれば、前者が1/4、後者が3/4で起きるので、
1*(1/4)+(1/3)*(3/4)=1/2
正解率50%となります。
(2)選択肢が2つ認識できる場合
分かる2つのどちらかが運よく正解選択肢ならば正解率100%、分からない2つのどちらかが正解選択肢なら正解率1/2です。
ここで[A]の仮定が成り立つ場合、前者が1/2(=2/4)、後者が1/2(=2/4)で起きるので、
1*(1/2)+(1/2)*(1/2)=3/4
正解率75%となります。
(3)選択肢が3つ認識できる場合
正解選択肢が、理解できる3つの選択肢のどれかだったときは必ず正解できます。そうでない場合は、正解は4つのうち必ず1つなので消去法で正解できます。
よって正解率100%です。
(4)選択肢が4つすべて認識できる場合
正解率100%です。
(問題文の意味を取り違えたり、回答に必要な情報を見逃したりしていなければ)
以上より、選択肢が\(n\)個\((n=0,1,2,3)\)分かる場合は正解率は\((n+1)/4\), \(4\)つすべて分かる場合は正解率\(1\)となります。
次に、選択肢認識率と4択問題で認識できる選択肢の数は次の通りです。
選択肢認識率と上の場合の条件分岐法則
ここで、問題の選択肢の中に「意味の分かる選択肢」が現れる確率(以下、選択肢認識率)を\(p\)とします。(※どの問題のどの選択肢についても、\(i.i.d.\)であると仮定)
このとき、上で書いたそれぞれ5つの場合になる確率はパラメータ\(4, p\)の二項分布\(Bin(4, p)\)に従うので、
(0):\((1-p)^4\)
(1):\(4p(1-p)^3\)
(2):\(6p^2(1-p)^2\)
(3):\(4p^3(1-p)\)
(4):\(p^4\)
となります。
以上より、選択肢認識率と正解率の関係は以下の通りです。
最終的な選択肢認識率と正解率の関係
このすべての場合それぞれに対して正解率をかけて足し合わせると、
\((1/4) \times (1-p)^4 + (2/4) \times 4p(1-p)^3 + (3/4) \times 6p^2(1-p)^2 + 1 \times 4p^3(1-p) + 1 \times p^4\)これを計算すると、結果的に\(p^2, p^3\)の項が消えて、
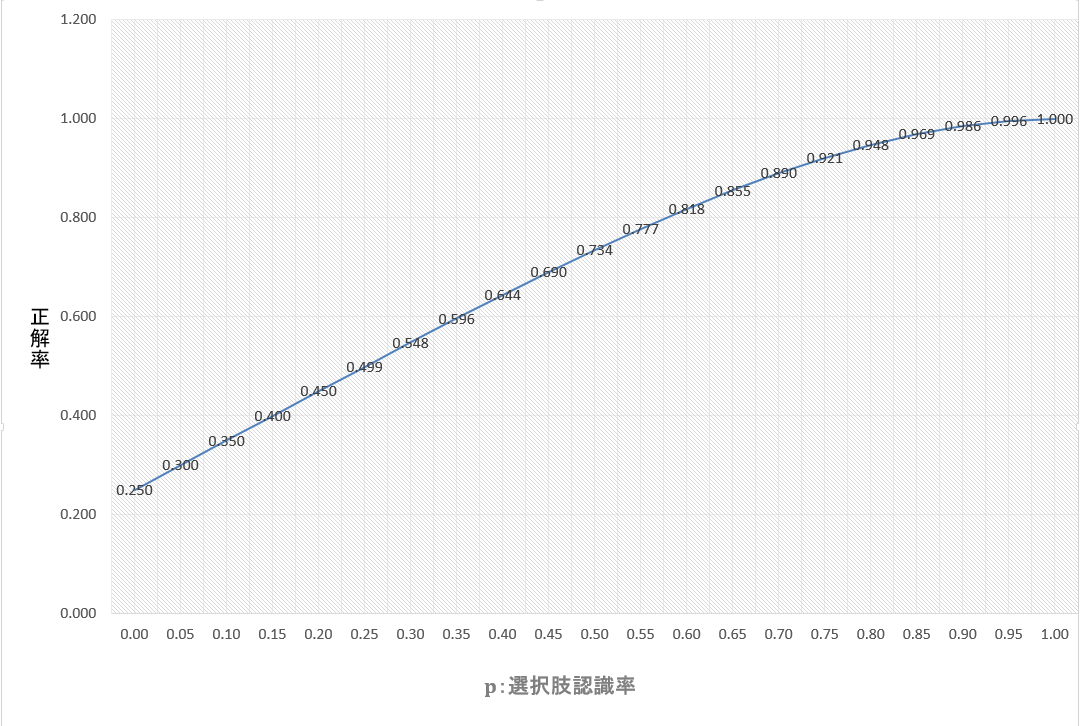
\(1/4+p-p^4/4\)となります。p:選択肢認識率をx軸、そして上記の正解率をy軸にとったグラフは以下のようになります。
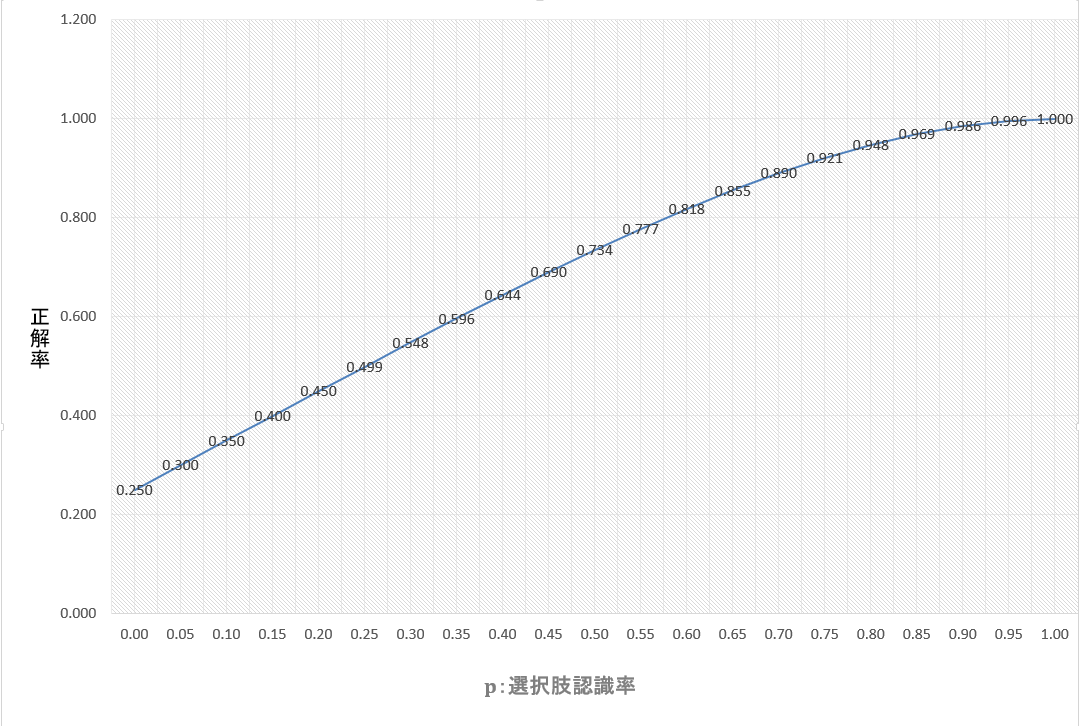
考察
このグラフについて、認識率0%では4択なので正解率25%、認識率100%では正解率100%。
認識率が低いときは\(p^4\)の項が小さく\(1/4+p\)に近いグラフとなり、認識率が高いときは\(p^4\)の項が大きくなり傾きが小さくなります。
つまり、認識率が低いときほど伸び率が高く、認識率が高くなってくると伸び率が悪くなってきます。(微分係数を調べてもわかります)
また、英検1級、準1級では合格のボーダーラインは全体正解率70%くらいと言われております。
上のグラフで正解率70%を超えるのは選択肢認識率46.2%のときで、約半分の割合で選択肢が認識できるときとなります。
認識率5割で正解率73.4%、6割で正解率81.8%、7割で89.0%、8割で94.8%、9割で98.6%。
そう考えると、語彙問題以外でそれなりに得点できる自信がある人は少なくとも選択肢認識率5割を目指すにとどめ、他の分野を頑張る、というのも1つの戦略としてありなのではないか、と考えられます。
注意点
この記事の結果は、以下の仮定が成立するとみなしたうえでの理想状態です。
・各選択肢が問題の答えになるかどうかを確実に判断でき、その確率(選択肢認識率)はどの問題に対しても一様に\(p\)で、独立同一分布である
・正誤判定できる選択肢であることと、問題の正解となる選択肢であることが互いに独立である
実際の試験では、問題の分野ごとに選択肢認識率が違ったり(科学分野は得意だが政治分野は苦手、あるいは問題ごとの難易度の差など)、問題の選択肢が似た意味の単語で、選択肢認識率がどう考えても独立でなさそうだったり(conserveとpreserveの微妙なニュアンスの違いなど)する問題もあります。
しかし、英検1級では各選択肢ごとの意味がほぼ違う、という問題が多いので理想状態からのずれはあまり大きくはない部類だと思います。
まとめ
・選択肢ごとの選択肢認識率\(p\)と問題の正誤との独立性等を仮定する理想条件下では、正解率は\(1/4+p-p^4/4\)となる
・この正解率が英検1級、準1級の1次試験合格ボーダーライン約7割を超えるのは選択肢認識率が約5割のとき
・英検1級語彙問題は難関だが、上記を考慮すると恐れる必要はなし。覚えた単語をある程度失念しても他でしっかりしていればなんとかなる

コメント