パワポケ10裏サクセス バトルディッガー編の主砲の性能は0-1の乱数値24個分によって決定されます。
本記事では、主砲の性能(攻撃、命中、素早さ、弾数の変動値)を目的変数、武器の性能決定に使った24個の乱数値を説明変数とした重回帰分析(※今回は線形回帰)を行い、主砲の性能の決まり方や強い主砲をゲットするための乱数列の探し方を模索します。
今回はデータ数31で解析を行いました。
データについて
データの取得
起動時間と乱数消費数を把握したうえでパワポケ10 バトルディッガー編で武器を拾い、その性能を攻撃, 命中, 素早さ, 弾数の順に記載し、そのときの乱数24個分を下のように記録します。
23,12,3,7 45129 ★★ 木下 0.9855840343024195 45130 ★★ 藤本 0.8425441831778898 45131 ★★ 久保 0.9433834361503411 45132 ★★ 木下 0.9848549521457987 45133 ★★ 中川 0.5633512247505073 45134 ★★ 山口 0.24633605235551492 45135 ★★ 増田 0.8971863377044914 45136 ★★ 今井 0.8139465673218459 45137 ★★ 菅原 0.9389593532319124 45138 ★★ 谷口 0.7887563999503688 45139 ★★ 石田 0.6696396463048779 45140 ★★ 野口 0.99569119172431 45141 ★★ 千葉 0.9548581187300527 45142 ★★ 小山 0.9039617198855315 45143 ★★ 丸山 0.8010160127048829 45144 ★★ 大西 0.17479840814157938 45145 ★★ 石川 0.35724311668595615 45146 ★★ 岡田 0.4069564390072425 45147 ★★ 杉山 0.8896133470442243 45148 ★★ 岩崎 0.9723365079640414 45149 ★★ 中川 0.5671096314192896 45150 ★★ 上野 0.8777229925988091 45151 ★★ 山本 0.0695411777855829 45152 ★★ 野口 0.9920747427558051
乱数24個については、【改良版】パワポケの内部乱数観測器をPythonで実装してみたのプログラム出力をコピペしたものです。
これでデータが1つ分。このセットをあと30回分行えば、データ数は31になります。
ただ、このままだと手前の★やオート命名の名前など、データ解析に余計な部分があるのでそれを取り除くべく、下の項の「データクレンジング」をします。
データクレンジング
データ解析ができる書式等に統一します。
データ分析の前処理となる作業です。(データクリーニングとも呼びます)
1:乱数24個分のうち、余計な部分を取り除く
0-1の乱数値24個分だけにするべく、左側の★やオート命名の名前を削除します。やり方は例えば、
EXCELの関数で以下を入力して先頭の9文字を削除します。(参考:https://www.offinet.com/news/entry_62325.html)
=RIGHT(A1,LEN(A1)-9)
その次に数字のみを取り出すべく、例えば以下を入力します。(セルの位置に注意)
=LOOKUP(10^17,RIGHT(F1,COLUMN(1:1))*1)
あとはドラッグで全31個の乱数データに適用すると、データ解析に必要な0-1の乱数値24個分が31セット取得できます。
2:主砲データをCSVから攻撃、命中、素早さ、弾数へ
23,12,3,7とコンマで区切られているものを、攻撃、命中、素早さ、弾数とします。
データ取得段階で空白区切りや改行で対応しておいた方がよかったかもしれませんが、コンマ区切りの数値(CSV)なら対応可です。(方法はググればたくさんある)
3:データを行列の形にする
結合、転置、ラベル付けetcをします。
最終的にデータを下のようにします。
攻撃 命中 素早さ 弾数 No1 No2 No3 No4 No5 No6 No7 No8 No9 No10 No11 No12 No13 No14 No15 No16 No17 No18 No19 No20 No21 No22 No23 No24 23 12 3 7 0.985584034 0.842544183 0.943383436 0.984854952 0.563351225 0.246336052 0.897186338 0.813946567 0.938959353 0.7887564 0.669639646 0.995691192 0.954858119 0.90396172 0.801016013 0.174798408 0.357243117 0.406956439 0.889613347 0.972336508 0.567109631 0.877722993 0.069541178 0.992074743 19 13 0 9 0.758625791 0.935228492 0.812879155 0.831614063 0.968332075 0.116843011 0.826392693 0.932970501 0.960169551 0.989519064 0.47806211 0.24761399 0.910527395 0.83805494 0.891113743 0.181678404 0.393547654 0.764804076 0.82030015 0.908102419 0.081393393 0.104959721 0.083277584 0.435253447 21 13 1 11 0.88912043 0.852777668 0.800923473 0.712547879 0.698768016 0.996054359 0.989635897 0.480576158 0.851623839 0.816763957 0.825075326 0.967765702 0.945383818 0.809793446 0.994361975 0.920195984 0.950608579 0.940512661 0.719344327 0.758670939 0.65181531 0.215622103 0.62508959 0.872317711 18 11 3 11 0.637153321 0.977479434 0.593716613 0.913966783 0.840628065 0.324827919 0.791550258 0.937460818 0.698115459 0.568236017 0.810019468 0.973517055 0.954537214 0.004052705 0.938321597 0.434481089 0.882909255 0.941305233 0.965163559 0.988615222 0.908605556 0.926265903 0.861722381 0.924902998 20 13 1 11 0.791550258 0.937460818 0.698115459 0.568236017 0.810019468 0.973517055 0.954537214 0.004052705 0.938321597 0.434481089 0.882909255 0.941305233 0.965163559 0.988615222 0.908605556 0.926265903 0.861722381 0.924902998 0.633659624 0.979250677 0.028323954 0.41327617 0.583144188 0.783956143 22 11 2 11 0.949717826 0.943037656 0.842717349 0.653717632 0.767300974 0.901668221 0.698533176 0.906037968 0.707427286 0.876616384 0.715196811 0.981435495 0.99290326 0.82638243 0.538565479 0.804074257 0.998452416 0.958712051 0.877492644 0.770149854 0.852115711 0.490443002 0.283584027 0.572685238 23 12 0 7 0.936600246 0.945879995 0.98368707 0.926024422 0.154486633 0.51225213 0.936663909 0.995397485 0.615173426 0.75927354 0.699245752 0.926797663 0.995851799 0.973862924 0.240697496 0.118531777 0.453430483 0.031663286 0.677366346 0.613776438 0.09118533 0.00497658 0.451155717 0.331397985 22 11 2 10 0.88921673 0.926090729 0.888152483 0.960487755 0.918591852 0.970725049 0.680453776 0.999227827 0.909823947 0.92924956 0.843798476 0.439579005 0.999913554 0.64641606 0.904359853 0.907761175 0.825759752 0.729149762 0.971376455 0.835256206 0.563672582 0.077244528 0.521207307 0.58658353 23 13 1 10 0.895260007 0.683091633 0.932018126 0.789934987 0.99398473 0.933837005 0.995878396 0.910628646 0.835764372 0.810004825 0.733427503 0.965292362 0.938689607 0.956131572 0.779900677 0.975199913 0.490405715 0.817113046 0.623773556 0.880413408 0.09097949 0.858890624 0.436110813 0.069943266 23 13 0 11 0.97619436 0.877197789 0.788781947 0.976926526 0.92128982 0.962540269 0.941686617 0.961247816 0.595888294 0.531106084 0.914221246 0.895990496 0.874829303 0.860889252 0.9425245 0.689806676 0.949499149 0.946609629 0.297524137 0.310966601 0.882457453 0.676040279 0.15553956 0.628277491 22 13 2 11 0.959293502 0.368014021 0.969864316 0.560717621 0.928883483 0.823654717 0.942713418 0.71127684 0.978360853 0.854327713 0.525069641 0.956620224 0.993101821 0.921506575 0.845295378 0.965244338 0.679635495 0.135720318 0.871048657 0.140721851 0.900849584 0.926528338 0.754636624 0.57112753 23 11 1 9 0.951363351 0.889168203 0.951365813 0.806060993 0.901657889 0.984697274 0.695505547 0.959546544 0.931140089 0.814389539 0.871581091 0.989776516 0.777281511 0.658151374 0.735250634 0.902243774 0.914047956 0.894739026 0.316015526 0.990608407 0.865400425 0.953872605 0.971944451 0.901251883 22 12 2 9 0.995969457 0.870568746 0.884285144 0.900790074 0.722401704 0.886398423 0.908795596 0.975505534 0.796635201 0.748037524 0.744202119 0.998866808 0.937035274 0.7331667 0.544171413 0.846571293 0.697769559 0.877551788 0.993811111 0.667540867 0.855086563 0.602419561 0.68818379 0.604835552 24 12 2 8 0.972757279 0.92050427 0.952994774 0.823424122 0.982042461 0.573266869 0.939391098 0.853215859 0.940192109 0.919157386 0.050197307 0.697082455 0.946564748 0.944538053 0.907683418 0.473594296 0.507832481 0.189185018 0.87069216 0.951998901 0.269508362 0.069834 0.564983643 0.558252841 22 14 2 10 0.97503935 0.998434193 0.901383583 0.819843925 0.44669898 0.79194731 0.999419833 0.990829501 0.864790749 0.056649548 0.373570761 0.947126622 0.957708264 0.940771927 0.823150503 0.217920101 0.497523156 0.702287432 0.971978896 0.559487382 0.081799318 0.505808107 0.166495915 0.935616118 24 14 2 10 0.986874119 0.95833412 0.970880371 0.727472538 0.371050543 0.929919881 0.96949424 0.921441664 0.948092857 0.035067578 0.511370009 0.982112038 0.979759095 0.884764375 0.862702921 0.676165956 0.857331185 0.575184715 0.932502678 0.745896177 0.621475451 0.840202202 0.419673683 0.547314046 24 14 0 11 0.953893551 0.988262621 0.998576988 0.781587104 0.0058768 0.934257027 0.992551247 0.985606938 0.90657612 0.226712176 0.004768058 0.946583556 0.91711382 0.923361529 0.933782347 0.913973521 0.999886451 0.525046196 0.197101751 0.962575038 0.325789415 0.823105364 0.307509983 0.697947534 22 13 1 10 0.968423768 0.931473549 0.727272149 0.998878435 0.028321275 0.833204185 0.982522927 0.992550284 0.849862412 0.787135004 0.323934368 0.913852237 0.953901472 0.917508816 0.863524881 0.73701319 0.058122219 0.768545676 0.09976075 0.889439 0.991234533 0.998184738 0.738002924 0.604885848 22 14 1 10 0.927052833 0.889377148 0.864791969 0.931568314 0.937965309 0.90322225 0.975736288 0.808673014 0.983422132 0.88737183 0.88757032 0.980502981 0.933704032 0.856475694 0.840336451 0.531468978 0.725597451 0.922605468 0.992800498 0.695660018 0.008712009 0.633949103 0.317567453 0.520020795 22 14 0 9 0.91353797 0.998908674 0.932017945 0.806103952 0.883986377 0.730686768 0.942822322 0.989452066 0.99799804 0.446618273 0.559112428 0.99265315 0.793238249 0.943618263 0.977328156 0.730018174 0.777276526 0.532249166 0.33069436 0.744819113 0.206314103 0.253110654 0.964241053 0.266828247 22 14 -1 10 0.938954019 0.942968817 0.911396505 0.827647511 0.566373224 0.930178357 0.997784525 0.895598527 0.986477252 0.435484271 0.889747807 0.971687273 0.948248454 0.869186293 0.923908301 0.856031338 0.435549482 0.781420197 0.201659642 0.780966663 0.320340302 0.644489259 0.475970639 0.402167942 23 14 0 10 0.987763189 0.913308586 0.936873652 0.910702515 0.774955048 0.936769909 0.977043379 0.86846402 0.994636082 0.94538674 0.873121508 0.99909793 0.921934765 0.99893127 0.701249835 0.515995329 0.547362948 0.775739266 0.203642014 0.791182667 0.874052924 0.293958602 0.58539437 0.636263485 21 14 1 8 0.968857282 0.980546209 0.707825725 0.964217601 0.173758677 0.7730296 0.945081614 0.907583001 0.99279611 0.473832787 0.546573909 0.984563175 0.994950943 0.692142428 0.963970349 0.204818338 0.20709809 0.413879542 0.968096562 0.790530906 0.280317 0.36579605 0.212927756 0.161456773 23 13 1 8 0.911286289 0.927458262 0.992329442 0.78090246 0.519353203 0.95168787 0.857435352 0.861616919 0.945164747 0.207840639 0.946744912 0.975818786 0.920949555 0.921006627 0.850533739 0.411179274 0.0087363 0.514003812 0.925314484 0.163673666 0.685324295 0.753502874 0.072967547 0.454872718 25 3 0 4 0.996393405 0.99602635 0.998722863 0.992159514 0.963951432 0.159816245 0.221699002 0.694763046 0.962359051 0.162271978 0.075173332 0.573198051 0.476128168 0.504643532 0.760021119 0.656288125 0.606749827 0.130915467 0.030342971 0.410215496 0.481548927 0.582142944 0.970244777 0.421092771 -2 6 4 3 0.255747616 0.003585931 0.033175664 0.133757061 0.1213389 0.589915627 0.636872728 0.863857151 0.946341346 0.267904003 0.515601775 0.367481568 0.114094359 0.541937662 0.967275516 0.162701545 0.483446162 0.175348854 0.948181887 0.987206696 0.99650285 0.987050098 0.949442654 0.993088475 13 1 1 12 0.636872728 0.863857151 0.946341346 0.267904003 0.515601775 0.367481568 0.114094359 0.541937662 0.967275516 0.162701545 0.483446162 0.175348854 0.948181887 0.987206696 0.99650285 0.987050098 0.949442654 0.993088475 0.224033442 0.435215745 0.562831256 0.965351592 0.726080704 0.922261149 10 9 2 12 0.946341346 0.267904003 0.515601775 0.367481568 0.114094359 0.541937662 0.967275516 0.162701545 0.483446162 0.175348854 0.948181887 0.987206696 0.99650285 0.987050098 0.949442654 0.993088475 0.224033442 0.435215745 0.562831256 0.965351592 0.726080704 0.922261149 0.520559689 0.840416889 19 13 2 9 0.643834749 0.984126435 0.933840396 0.888171007 0.983522445 0.943103509 0.920409329 0.697328889 0.919339285 0.945869127 0.822756085 0.989561431 0.861106607 0.807910724 0.931033136 0.803308818 0.301664843 0.761332989 0.850230569 0.765513513 0.941402658 0.823973727 0.823961919 0.264145053 23 12 2 10 0.986596023 0.842593027 0.983581946 0.892109875 0.218026474 0.958914911 0.981004053 0.775772095 0.562486476 0.956487549 0.859383961 0.642280227 0.951218249 0.969124063 0.682162649 0.166619271 0.751799612 0.805619271 0.725868518 0.929478131 0.724097012 0.901452934 0.993949179 0.17937445 23 14 2 7 0.934855187 0.894803258 0.888812665 0.6166314 0.671750455 0.972233124 0.978756109 0.832557457 0.768553668 0.890822668 0.911815927 0.987184073 0.663202384 0.481042787 0.91980917 0.657352514 0.910126181 0.325814195 0.824477354 0.7742386 0.864702188 0.624156109 0.661675885 0.356747678
このデータをもとに分析をします。
重回帰分析
攻撃、命中、素早さ、弾数についてEXCELで重回帰分析をします。
やり方や参考サイトは
【秒で使える】重回帰分析をエクセルの分析ツールでやってみよう
あたりを参考にしてください。
結果
24個の乱数値のうち、経験上攻撃が1-6番目、命中が7-12番目、弾数が13-18番目、素早さが19-24番目のものを使っている説が有力なので、その前後の乱数値を説明変数として分析しました。
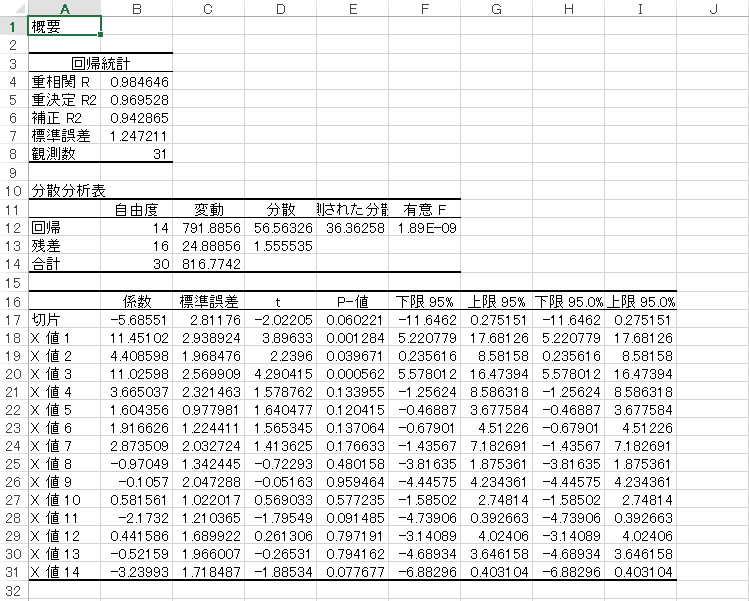
攻撃
B18, B20の値を見ると、1, 3番目の乱数の大きさが特に攻撃力決定に大きく寄与していることが分かります。
分散分析表の見方の参考は例えばこちら(https://www.netyear.net/idea/data20180117.html)
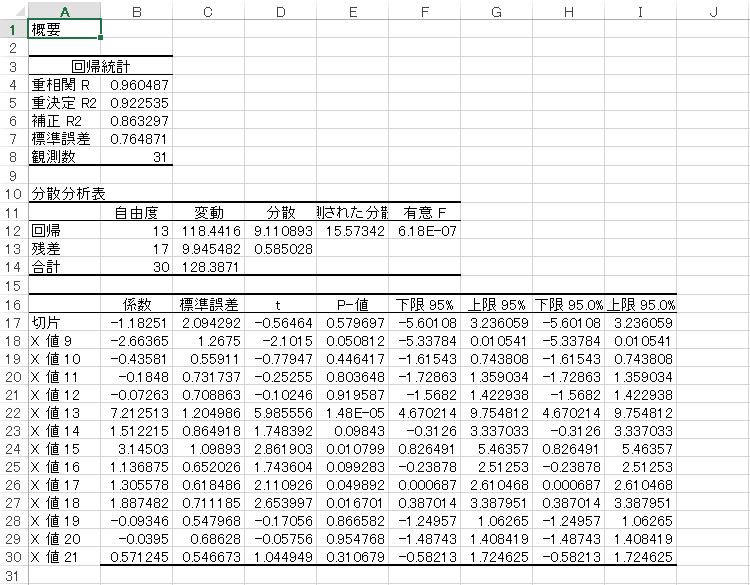
命中
7番目の乱数値が大きく命中アップに寄与しています。
8, 9番目も有意に命中アップに貢献か。(p値や下限95%と上限95%の範囲を見ればOK)
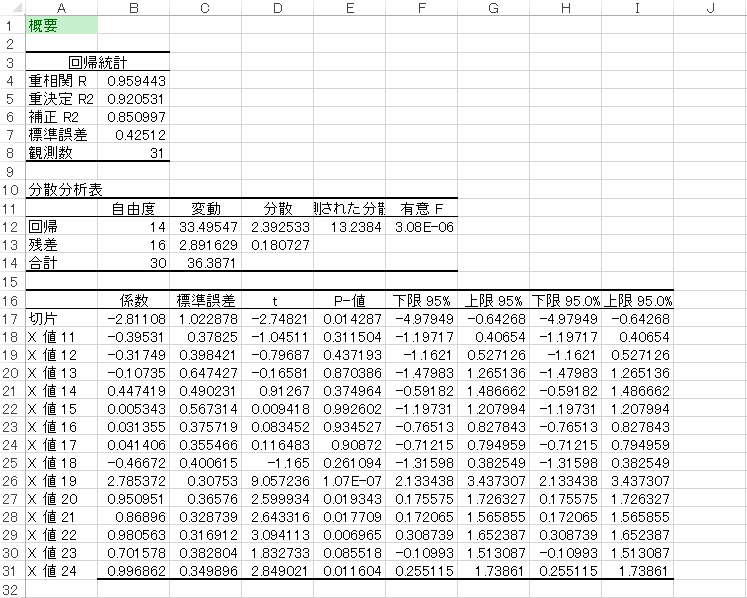
弾数
13番目が大きく貢献、14-18番目も貢献しているようです。(有意かというとまだ微妙なものもある)
素早さ
19番目の貢献度が大きく、20-24番目も同じく素早さアップに貢献。
弾数と同じ感じの構成パターンですね。
再び乱数探索へ
分析結果から、係数の値を重みとした重み付き和を特徴量として一定以上の基準を満たす乱数値を探索(筆者の「パワポケ 乱数」タグのついた記事などを参照)をし、その乱数で武器を生成してみます。
結果
攻撃、命中、素早さ、弾数の順番です。(現時点で総合的に最高の性能のものは23,13,3,10)
23,6,3,11 20,8,3,10 20,14,2,11 19,13,2,10 24,12,2,11 22,13,2,10 20,14,3,10 22,14,3,10 21,12,2,11 21,13,2,11 22,12,2,9
最初の方は乱数探索(メタヒューリスティック)をするときの足切りが甘すぎたりする場面もあったりしましたが、おおむね高い水準の武器を生成できています。(特に弾数)
本記事執筆時点で総合的に最高である23,13,3,10を超えるためには
説明変数を変えて再度分析
適切な乱数値を説明変数へ追加、削除をして分析を繰り返すことで汎化性能の向上や過学習の回避を図ります。
1-24番目の乱数値で決まるのは99.9%確定なのでそれすべてでやるか、あるいは経験的な値(攻撃が1-6番目、命中が7-12番目、弾数が13-18番目、素早さが19-24番目)のみでやるかなど。
データの質、量の向上
乱数値を記録している主砲は高性能のものばっかりです。(乱数調整等をしないと現在の乱数値の把握が困難、記録およびデータ収集もできないため)
つまり、「ランダムにサンプリングしている」状態ではないということです。
できれば悪性能や普通の性能など幅広く、ランダムにデータを取りたいところでした。
F値が十分小さいので今のままでも問題ないかもしれないですが・・・
乱数探索時のパラメータ変更
上の説明変数に係数を重みづけした和の値(=目的変数)が一定以上を満たす乱数値を出力、という形で乱数探索をしていますが、その一定の基準(足切り)を厳しくする方法です。
乱数探索で足切りを厳しくするのは、現実的な探索時間や乱数調整時間を維持するのが困難なので過度にするのは難しそうなので、できればこれは最終手段にとどめたいところ。
最後に
重回帰分析で求めた係数を重みづけの値とした乱数探索によって通常時では滅多にお目にかかれない性能のものができることを確認しました。24,12,2,11や22,14,3,10ものならまだ現行の最高値23,13,3,10と張り合えるレベル。
単体のパラメータだけならそれ以上のものはいくつもありますが、総合的に超えるには今回の結果をもとに前項などの改善を続けていくことがまだ必要そうです。
特に強い主砲をゲットするための乱数はパワポケ10 強い主砲をゲットするための乱数まとめにあります。
23,13,3,10を超えるものを見つけた方はコメントお待ちしております。


コメント